Introduction
Yup, it’s that time of the year again, the festive season! Christmas trees, lights, decoration, … and the Advent of Code! If you’re not familiar with the Advent of Code, well, it’s a puzzle game for programmers during the advent.
Each day, you get a new challenge, written as part of a bigger story. The goal of these challenges it to find the result by using your programming skills.
The challenge
With todays challenge, we get a list of coordinates that contain a mark on a paper. In addition, we also get a list of folds that have to happen.
Each time we fold the paper, we have to translate the marks from one side of the paper to their counterpart on the other side of the fold.
Part one
Part one of the challenge is to find out how many marks remain after folding the paper a single time.
Marks can disappear if they’re on the fold line, or if the mark appears on the same spot on both sides of the fold.
For example:
#....
.....
-----
.....
#....
In this example, the paper initially has two marks, on the top left and bottom left corner. If we fold the paper in half, the top and bottom mark will appear on the same position, and we end up with a single mark left:
#....
.....
Value objects
To implement this, I first wrote a Coordinate class:
@With
@Value
public class Coordinate {
int x;
int y;
public static Coordinate fromLine(String line) {
String[] parameters = line.split(",");
return new Coordinate(parseInt(parameters[0]), parseInt(parameters[1]));
}
}
This immutable class contains two fields, being the X and Y coordinate.
In addition, it has a fromLine() static method, that generates a Coordinate based on the input we get (wich is a comma separate X and Y value within a file).
Similar to this, I wrote a FoldInstruction class:
@Value
public class FoldInstruction {
FoldType type;
int value;
public static FoldInstruction fromLine(String line) {
String foldTypeSymbol = line.substring(11, 12);
String valueString = line.substring(13);
return new FoldInstruction(FoldType.valueOf(foldTypeSymbol.toUpperCase(Locale.ROOT)), parseInt(valueString));
}
public boolean isXType() {
return FoldType.X.equals(type);
}
public boolean isYType() {
return FoldType.Y.equals(type);
}
private enum FoldType {
X, Y
}
}
This class is a bit more complex since we can fold either horizontally or vertically. I didn’t like using a boolean here, so I used an enum with two values. In stead of naming the values horizontally and vertically, I decided to follow the same naming convention as used within the challenge, which is:
fold along y=7
fold along x=5
Writing the logic
After that I declared a TransparentPaper class. My first attempt was to create a boolean array where each coordinate would either be true if it was marked, or false if it wasn’t.
But then I decided that this would be a waste of computation power, since we’re only interested in which coordinates are marked.
So in stead of that, I started with a list of marked coordinates:
@Value
public class TransparentPaper {
List<Coordinate> marks;
public static TransparentPaper fromLines(List<String> lines) {
List<Coordinate> marks = lines
.stream()
.map(Coordinate::fromLine)
.collect(toList());
return new TransparentPaper(marks);
}
}
The next part is to write the folding logic.
First, I wrote a method to calculate the translation for a single coordinate:
private Optional<Coordinate> calculateCoordinateAfterFold(Coordinate coordinate, FoldInstruction instruction) {
if (instruction.isXType()) {
int distanceFromLine = Math.abs(instruction.getValue() - coordinate.getX());
if (distanceFromLine > 0) return Optional.of(coordinate.withX(instruction.getValue() - distanceFromLine));
else return Optional.empty();
} else if (instruction.isYType()) {
int distanceFromLine = Math.abs(instruction.getValue() - coordinate.getY());
if (distanceFromLine > 0) return Optional.of(coordinate.withY(instruction.getValue() - distanceFromLine));
else return Optional.empty();
} else {
return Optional.empty();
}
}
I made a lot of mistakes in this part. One of the mistakes I made is that I made the assumption that the paper would always be folded in half. In the example given during the challenge, this is the case. However, this isn’t true for the larger dataset.
So, to translate the X and Y coordinate, you have to calculate the distance from the fold line, and subtract that from the fold line itself. One edge case is when the distance is zero. That means that the coordinates are on the fold line itself, and should be scrapped.
To solve this, I decided to return an Optional that would be empty when the coordinate is on the fold line.
After that, I wrote a fold() method that would apply a single fold and return a new TransparentPaper instance.
public TransparentPaper fold(FoldInstruction instruction) {
List<Coordinate> newMarks = marks
.stream()
.map(coordinate -> calculateCoordinateAfterFold(coordinate, instruction))
.flatMap(Optional::stream)
.distinct()
.collect(toList());
return new TransparentPaper(newMarks);
}
Within this method, we call the calculateCoordinateAfterFold() method for each mark, remove the duplicates and return a new instance of TransparentPaper.
The reason I chose to make a new one is because I prefer using immutable classes.
The final part is to write a method that returns the amount of marks there are:
public int calculateMarkCount() {
return marks.size();
}
Testing the result
According to the challenge, the example we get should return 17 marks after applying the first fold.
So, to verify this I wrote a unit test:
@ParameterizedTest
@CsvSource({
"/day13_sample.txt,17"
})
public void partOne(String fileLocation, int expectedOutput) throws URISyntaxException, IOException {
List<String> lines = readLines(fileLocation);
List<List<String>> parts = splitLinesByEmptyLine(lines);
List<String> paperMarkCoordinates = parts.get(0);
List<String> foldInstructions = parts.get(1);
TransparentPaper paper = TransparentPaper.fromLines(paperMarkCoordinates);
FoldInstruction instruction = FoldInstruction.fromLine(foldInstructions.get(0));
TransparentPaper result = paper.fold(instruction);
assertThat(result.calculateMarkCount()).isEqualTo(expectedOutput);
}
What happens here is that I first read all the lines from the given file. After that, I split the lines into two parts:
- The first part containing only the lines with coordinates.
- The second part containing only the lines with fold actions.
Then I create a TransparentPaper and FoldInstruction instance by using the static methods I wrote.
After that I applied a single fold and called the calculateMarkCount() method to verify that the result matches 17.
When that worked, I added the full example to the @CsvSource annotation:
@ParameterizedTest
@CsvSource({
"/day13_sample.txt,17",
"/day13_full.txt,0" // Add this
})
public void partOne(String fileLocation, int expectedOutput) throws URISyntaxException, IOException {
// ...
}
This test will fail, because there will be more marks than zero. JUnit will then tell me what the result should be, and that’s what I entered.
Part two
The next part is to print out the result after applying all folds. This should result into a series of upper case letters, which is the answer to the second part of the challenge.
Writing the logic
Now, since we only have a list of marked coordinates, this will take a bit more computational power.
First of all, we have to determine what the width and height of our paper will be. The way we calculate this is by calculating the highest X and Y coordinate, and incrementing those by one:
public int calculateWidth() {
return marks
.stream()
.mapToInt(Coordinate::getX)
.max()
.orElse(0) + 1;
}
public int calculateHeight() {
return marks
.stream()
.mapToInt(Coordinate::getY)
.max()
.orElse(0) + 1;
}
After that, we can print it by creating a list of all possible coordinates within that area, and checking whether they’re within the marks.
If they are, then we print a hashtag, if not, we print a space.
The method I wrote is the following:
public void print() {
int width = calculateWidth();
int height = calculateHeight();
IntStream
.range(0, height)
.mapToObj(y -> IntStream
.range(0, width)
.mapToObj(x -> new Coordinate(x, y))
.map(coordinate -> marks.contains(coordinate) ? "#" : " ")
.collect(Collectors.joining()))
.forEach(System.out::println);
}
Testing it out
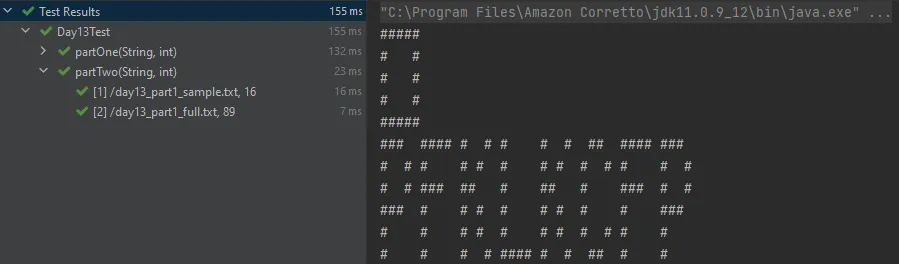
Writing a test for this is a bit more difficult. In stead of writing a test that interpretes the printed output, I decided to just print it during the test, and write an assertion based on the expected amount of marks. This is similar to part one, except that we now have to apply all folds in stead of a single one.
The way I implemented this is by using the reduce() operator:
@ParameterizedTest
@CsvSource({
"/day13_part1_sample.txt,16",
"/day13_part1_full.txt,0"
})
public void partTwo(String fileLocation, int expectedOutput) throws URISyntaxException, IOException {
List<String> lines = readLines(fileLocation);
List<List<String>> parts = splitLinesByEmptyLine(lines);
List<String> paperMarkCoordinates = parts.get(0);
List<String> foldInstructions = parts.get(1);
TransparentPaper result = foldInstructions
.stream()
.map(FoldInstruction::fromLine)
.reduce(TransparentPaper.fromLines(paperMarkCoordinates), TransparentPaper::fold, unsupported());
result.print();
assertThat(result.calculateMarkCount()).isEqualTo(expectedOutput);
}
The reduce() stream operator allows you to start from a specific point (the initial paper) and apply multiple small increments to it (each fold) to return a single result.
However, since streams can be run in parallel, you also need to provide a third argument, which is a way to combine multiple partial results (partial TransparentPapers) together.
Since this increases the complexity, I decided to not use parallel streams and just throw an exception when the combiner is called.
Once the final TransparentPaper is generated, I print it, and then call calculateMarkCount() to assert whether the mark count matches the expected amount.
From the given sample, I manually counted the amount of marks that are left in the final folded paper, which is 16.
Conclusion
Personally, this was the hardest challenge for me so far this year. As usual, the full code can be found on GitHub.
